Arc of a Circle
Arc of a Circle: Overview
This topic covers concepts such as central angle, measure of an arc, property of sum of measures of arcs, chords corresponding to arcs theorem, and inscribed angle.
Important Questions on Arc of a Circle
Prove angles inscribed in the same arc are congruent.
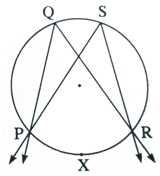
The inscribed angle in an arc of a circle if its vertex is out side the circle.
In the given circle arc and if chord , then find the value of chord in .
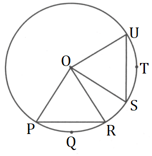
Prove that the chords corresponding to congruent arcs of a circle are congruent.
In the given circle chord . If and arc , find the value of arc in .
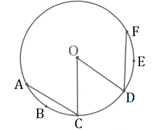
Prove that corresponding arcs of congruent chords of a circle are congruent.
In the circle, the points and are concyclic, then how many common point(s) do arc and arc have if
If the measure of the angle and the length of the radii of two arcs are equal, then the arcs are _____
Two arcs can be called congruent only and only if they have the same degree measure.
Prove that angles inscribed in the semi circle are right angle.
Prove that angles inscribed in the same circle are congruent.
If the measure of angle , then find the value of .
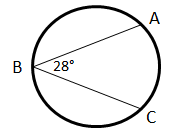
If the measure of angle , then find the value of .
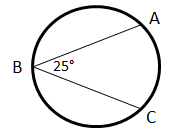
If the measure of angle , then find the value of .
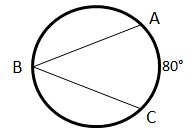
If the measure of angle , then find the value of .
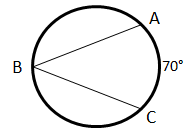
If the measure of angle , then find the value of .
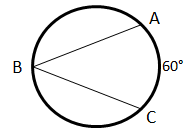
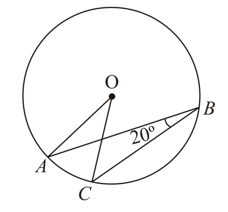
In the following figure, is the centre of the circle. is inscribed in arc and . Find the measure of .
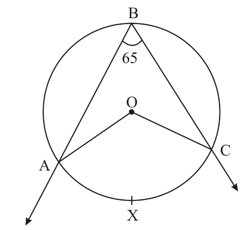
In the adjoining figure, is the centre of the circle. If ,then equal to